Vertical Circular Motion

A small sphere is attached to a cord and rotates in a vertical circle about a point $O$. If the range speed of the sphere is increased, the cord is most likely to break at the orientation when the mass is at:

A stone tied to a string is rotated in a vertical circle. The minimum speed of the stone during a complete vertical circular motion 

A small block is shot into each of the four smooth tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in

A point mass $\mathrm{M}$ is hanging by a string of length $\mathrm{l}.$ The velocity $v$ which must be imparted to it in order for it to just barely reach the top is

A pendulum is made of a rigid rod (mass $m,$ length $l$ ) and a small bob of mass $M$ attached at one end (as shown in the figure). The rod is pivoted on the other end. What should be the minimum speed of the bob at its lowest point so that the pendulum completes a full circle ?

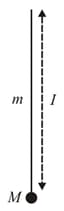
A particle is released on a vertical smooth semicircular track from point $X$ so that, $OX$ makes angle $\mathrm{\theta }$  from the vertical (see figure). The normal reaction of the track on the particle vanishes at the point $Y$ where $OY$ makes an angle $\mathrm{\varphi }$ with the horizontal. Then

The bob of a pendulum of mass $m$ and length $L$ is displaced $90°$ from the vertical and gently released. In order that the string may not break upon passing through the lowest point, its minimum strength must be

A particle of mass $m$ begins to slide down a fixed smooth sphere from the top. What is its tangential acceleration when it breaks off the sphere?

A particle is moving in a vertical circle. The tensions in the string when passing through two positions at angles $30°$ and $60°$ from vertical (lowest positions) are $T_1$ and $T_2$, respectively. Then

A mass $m$ is attached to a thin wire and whirled in a vertical circle. The wire is most likely to break, when

Concrete mixture is made by mixing cement, stone and sand in a rotating cylindrical drum. If the drum rotates too fast, the ingredients remain stuck to the wall of the drum and proper mixing of ingredients does not take place. The maximum rotational speed of the drum in revolutions per minute (rpm) to ensure proper mixing is close to:
(Take the radius of the drum to be $1.25 \mathrm{m}$ and its axle to be horizontal):

A pendulum string of length $𝓁$ moves up to a horizontal position as shown in figure and released.




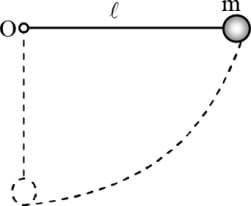
What should be the minimum strength of the string to withstand the tension as the pendulum passes through the position of equilibrium? The mass of the pendulum is $m$.

A particle slides from the top of a smooth hemispherical surface of radius R which is fixed on a horizontal surface. If it separates from the hemisphere at a height h from the horizontal surface, then the speed of the particle is:

A particle is tied to a string describes a vertical circular motion of radius $r$ continually. If it has a velocity $\sqrt{3gr}$ at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is

A bucket, full of water is revolved in a vertical circle of radius $1.5 \mathrm{m}.$ The maximum time period of revolution so that the water doesn't fall out of the bucket is $\left(g\approx {\pi }^2\right)$

A particle is attached at one end of a string of length $l$ whose other end is fixed. It is moving in a circular path in the vertical plane such that at any position. The tension in the string is $T$ and the acceleration of the particle is $a$. The velocity of the particle at the lowest point is $u$. Then find the condition at which $\overrightarrow{T}·\overrightarrow{a}$ will be positive at the lowest point.

A bob of mass $m$ of a simple pendulum of length $l$ displaced from position $O$ to $P$. $P$ is $h$ height above the position $O$. Then it is released from the position $P$. The velocity of the bob is $v$ at $O$. Find the tension in the string when the bob passes through the equilibrium position $O$ (neglect friction).

A simple pendulum is made by suspending a bob with a light string. The bob is imparted a horizontal velocity such that it just completes full circular trajectory in vertical plane. What is the difference in tension between lowest and highest point of path?

 A pendulum has an angular amplitude $\theta$. Tensions in the string when the pendulum is at the extreme position and at the bottom are $T_1$ and $T_2$ respectively. If $T_2=2T_1$ , then $\theta$ is equal to :-